漫长的告别

0%

Book Reading: CSAPP, Chapter 2, 整数的表示和运算

Posted on In , Views: Valine:
Symbols count in article: 4.5k Reading time ≈ 4 mins.

整数的表示

无符号数与有符号数

无符号数的表示非常直接，因为没有符号，k位的二进制就表示0 ~ 2k - 1范围内的整数。对于 [xk - 1, xk - 2, …, x0]，其表示的值为：

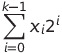
有符号因为存在负数的原因，其是用补码表示的。具体来说，其最高有效位的权重是负的，同样对于[xk - 1, xk - 2, …, x0]来说，其表示的值为:

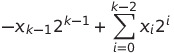
对于k位的二进制，其表示的有符号数的范围是-2k - 1 ~ 2k - 1 - 1。这个范围是非对称的，这个非对称性的来源是0。对于补码来说，所有最高位为1的表示负数，所有最高位为0的表示非负数，因为0也被包含在最高位为0的所有二进制当中，所以有了这种左右区间的不对称性。

为什么用补码表示有符号数

首先补码只是有符号数的一种编码方式，当然如果你愿意的话也可以尝试开发有符号数的其他编码方式。补码被广泛地应用主要是因为其能提供很多好处：

  1. 简化了了整数减法和负数加法的运算，在底层都可以用二进制的加法实现。这点之后会讲。
  2. 统一了有符号数和无符号数的运算在二进制层面的实现，使得两种数的四则运算几乎可以使用同一套规则。（唯一的例外是除法，之后会讲。）
  3. 符号位可以参与运算，同样下面会讲。

另外我们知道非负数的补码就是其二进制表示，而负数的补码是其反码（除符号位逐位取反）加一。诚然对于一个负数，我们可以用上面的公式推导出其补码，但为什么补码和其原码有这样的关系呢？我们将在下面讲解。

值得一提的是，C语言的标准并没有规定有符号数要用补码实现，但事实上，几乎所有机器都是这么做的。Java语言则在标准中严格规定了有符号数必须用补码实现，当然Java中也并没有无符号数，也就是说Java中所有的整数都是用补码表示的。

无符号数和有符号数的转换

字长相同的有符号和无符号数之间的转换遵循一个标准：二进制的表示不变，解码的方式改变。比如对于32位全为1的二进制数，其对应的无符号十进制数为232 - 1 = 4294967295，有符号数的十进制为-1。

另外，在C语言当中，如果对有符号数和无符号数做某种运算操作（加法、减法等），有符号数会被隐式转换为无符号数，这样很容易造成一些bug。例如-1 < 0U会被判定为false.

位数的扩展与截断

当在字长不同的整数型数据当中进行转换的时候，不可避免地我们需要进行位的扩展和截断的操作。当把无符号数转化成更大的字长的数时，只需要在二进制前面加上一串零即可，这样不会改变无符号数的值。

对于有符号数，我们则是在前导加上对应的符号位。对于正数，和无符号数类似，其表示的值没有受到影响。对于负数，假设其原来为k位，扩展之后加了n位前导1，那么总共变成了n + k位：

  1. 因为是负数，原来的k位补码，最高位肯定是1。假设剩下的k - 1位的和为C，那么其表示的十进制为-2k - 1 + C。
  2. 当加了n位前导0时，从第0位到第k - 2位的和仍然是C。从第k - 1位到第n + k - 1位的和为-2n + k - 1 + 2n + k - 2 + … + 2k - 1 = -2k - 1，那么加起来表示的数仍然为-2k - 1 + C。

我们讨论了在相同字长下，有符号数和无符号数之间的转化；以及，对应的无符号数和有符号数，在不同字长下的转化。那么如果同时进行了无符号数和有符号数，以及字长的转化，结果会是怎么样呢？我们考虑如下程序：

1
2
3
4
short sx = -12345; /* cf c7 */
unsigned uy = sx;

printf("uy = %u", uy);

这个程序的输出结果为：

1
uy = 4294954951 /* ff ff cf c7 */

在32位系统下，short为16位，unsigned为32位。看到最后的输出结果，我们可以看出来是先对short做了位数的扩展，之后进行了相同字长下有符号数到无符号数的转换。

我们可以看到，位数的扩展，在不同的数据类型中间会用到；位数的截断，同理也可以在整数的类型转换中用到，此外处理运算的溢出的时候也会用到。对于截断操作而言，其本质上就是在做模运算。假设从n位截断到k位（n > k）：

  1. 对于无符号数，截断后的值y = x mod 2k。
  2. 对于有符号数， 由于舍弃高位可能会导致符号改变，y = convertToSignedNum(x mod 2k)。

整数的运算

加法和减法

无符号数加法没有什么特别，唯一需要注意的是溢出的情况，这种情况会按字长截断，也就是取模。所以字长为k位的两个无符号数x，y，其和x + y = (x + y) mod 2k。

有符号数是用补码表示的，非负数的加法和无符号数是类似的。但是涉及负数的话就不太一样了，因为负数的加法本质上就是减法，这个时候补码的好处就出现了。

首先对于字长固定的类型，在溢出位被截断的情况下，其模是固定的，假设为M。对于负数来讲-x mod M = (M - x) mod M，这个很好理解，对于一个时钟，向前拨十个刻度和向后拨十个刻度最后的结果是一样的，都是指向10。我们把M - x定义为x的补数，我们可以看到，-x和M - X对于M来讲是同余的。

因为这个性质，在我们做整数的减法时，可以转化为其补数的加法。例如对于两个字长固定的正整数x，y来说，(x - y) mod M = (x + M - y) mod M，因为补数加法同余的性质，我们截断（取余）溢出位之后，这两个结果在二进制非符号位上的表示是一样的。例如：

1
2
3
4
x         15  0000 1111
y         125 0111 1101
M - y     3   0000 0011
x + M - y 18  0001 0010

加上符号位之后18 - 27 = 12 - 128 = -110 （1001 0010，正是对应减法的计算结果。如果我们直接把符号位带入M - y的话，对应的二进制就是1000 0011，是不是正好是-125的补码？同理：

1
2
3
4
x         125 0111 1101
y         15  0000 1111
M - y     113 0111 0001
x + M - y 238 1110 1110

由于最高位为符号位，溢出被截断，所以238 - 27 = 238 - 128 = 110 (0110 1110)，也是对应减法的计算结果。同理如果直接把符号位带入M - y，对应的二进制就是1111 0001，也是-15对应的补码。

我们可以看出来，直接把符号位带入的话，其二进制就是对应负数的补码，并且，符号位可以参与运算，不需要进行符号位的截断操作：

1
2
3
4
5
6
7
x     15   0000 1111
-y    -125 1000 0011
x - y -110 1001 0010

x     125 0111 1101
-y    -15 1111 0001
x - y 110 0110 1110

所以整数的减法可以在二进制层面用补码的加法实现，这样本质上整数的加法和减法，在二进制层面都变成了加法。这也就是为什么我们要用补码来表示符号数的原因。

另外值得一提的是，M - y = (M - 1) - y + 1，(M - 1) - y正好代表除了y的符号位全部取反，即反码；然后反码加一，变成了补码。

无符号数的减法也是类似的，那么显而易见地，在考虑溢出的情况下，k位无符号数和有符号数的加减法结果分别为（Tk代表只截取最低k位，TC(x)表示x的补码）：

  • 无符号数
    • x + y = Tk(x + y)
    • x - y = Tk(x + TC(Expanding(-y)))
  • 有符号数
    x ± y = Tk(TC(x) + TC(±y))

检测溢出

对于无符号数x, y和其和s来说，当且仅当s < x（此时y < x也必为真），计算发生了溢出。
对于有符号数x，y和其和s来说：

  • 当且仅当x > 0, y > 0并且s <= 0，计算发生正向溢出。
  • 当且仅当x < 0, y < 0并且s >= 0，计算发生负向溢出。

证明不难，这里略过。

乘法

乘法本质上还是加法，无符号数和有符号数的乘法在底层的运算逻辑还是一样的。对于k位的数，其乘法结果可能需要2k位才能表示，所以对于x和y来说，我们一般将其扩展到2k位，进行乘法运算，之后再截断。假设k为3：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
unsinged:

x 5 101
y 3 011

x * y = 000 101 * 000 011 = 001 111 = 15
Truncated x * y = 111 = 7

signed:

x -3 101
y 3  011

x * y = 111 101 * 000 011 = 110 111 = -9
Truncated x * y = 111 = -1

因为整数乘法的运算更加耗时，一般会耗费10个或者更多的时钟周期，而相对的整数的加减法，位操作等只需要一个时钟周期。编译器会对变量乘以一个常量的计算进行优化，思路是转化为位操作和加法，这样处理之后生成的机器码，就只需要进行位操作和加法，时间比做乘法要快很多。

首先我们看乘以2的幂，这个大家都知道可以用位操作左移来实现。不管对于有符号是还是无符号数，x * 2k都可以等价为x << k。那么对于任意常数C，因为其必定可以转化为2的幂的和，所以最后相乘的结果必定可以写出多个对x进行位操作左移的和。例如x * 14 = x * (23 + 22 +21)，那么其可以表示为(x << 3) + (x << 2) + (x << 1)。

同理14 = 24 - 21，x * 14也可以表示为(x << 4) - (x << 1)。

所以对于x乘以任意常数C，其可以表示为一系列的1和0（括号里的全为0或者1）：

[(0...0)(1...1)(0...0)...(111)]

例如14就可以表示为[(0...0)(111)(0)]。对于一段连续的1，假设从第n位到第m位（n >= m），我们可以将其表示为一下任意一种形式：

  1. (x << n) + (x << (n - 1)) + ... + (x << m)
  2. (x << (n + 1)) - (x << m)

除法

整数的除法比乘法还要慢，一般是30个时钟周期以上。但可惜的对于除以任意常量C，我们没有办法把其化为除以2的幂的和的形式，所以无法对其进行优化。但是对于除以2的幂的运算，我们还是可以用位操作进行优化。

因为可能无法整除的关系，我们首先定义整数的除法运算。对于任意实数a，我们首先定义⌊a⌋表示唯一的整数b使得b <= a < b + 1。例如⌊3.14⌋ = 3，⌊-3.14⌋ = -4。同理⌈a⌉表示唯一的整数b使得b - 1 < a <= b，例如⌈3.14⌉ = 4，⌈-3.14⌉ = -3。

那么对于任意整数x和y，当运算结果为正数时，结果应为⌊x / y⌋；而当结果为负数时，应为⌈x / y⌉。

那么这里有两种右移供我们选择，分别对应无符号数和有符号数的除法：

  1. 逻辑右移：在最高位补1，这种用在无符号数的除法。
  2. 算数右移：在最高位补符号位，这种用在有符号数的除法。

无论对于有符号数还是无符号数x >> k的结果都为⌊x / 2k⌋，所以对于结果为负的情况，我们要进行特殊处理:

当x < 0时，对于k >= 0, (x + (1 << k) - 1) >> k的结果为⌈x / 2k⌉。

这个也不难理解，我们分两种情况讨论：

  1. 当x正好能被2k整除，这后面加上的2k - 1在除以2k的时候会被舍去，所以结果为x / 2k = ⌈x / 2k⌉。
  2. 当x不能被2k整除时，x离⌈x / 2k⌉ * 2k的最大的差值就为2k - 1，所以加上之后再除就可以得到⌈x / 2k⌉。

所以对于有符号数x除以2的k次幂的结果可以表示为：

(x < 0? x + (1 << k) - 1 : x) >> k