Book Reading: CSAPP, Chapter 2, 浮点数的表示和运算

浮点数的表示

实数数的二进制表示

计算机用浮点数表示实数，二进制层面的表示和十进制是十分类似的：

其中在小数点左边的每一位有2^m权重，右边的每一位有2^-n的权重。所以每一个用如上方式表示的浮点数，其值为：

我们可以看出来，在有限长度编码的条件下，我们是没有办法精确表示任意实数的，比如说1 / 3或者5 / 7，所以只能近似表示。

IEEE754标准

如果我们用如上的编码方式在计算机中表示实数，那么其限制是很大的，比如5 * 2¹⁰⁰需要至少一百位来表示，在表示很大的数的时候不效率。所以IEEE标准规定了浮点数V的表示方法如下：

V = (-1)^s x M x 2^E

其中s，M和E分别表示：

s代表符号位，为1的时候表示负数，为0的时候表示正数。
M代表尾数(significand), 代表有效数字，可以理解成小数点还没移动时的数。
E代表指数(exponent)，或又称阶码，可以看到正是这个数决定了小数点是向左还是向右，会移动几位。

所以每一个浮点数的二进制表示，也会分为三个部分：

一位来表示符号位s。
长度为k的位数来表示指数部分E。
长度为n的位数来表示位数部分M。

例如，对于单精度和双精度浮点数，IEEE规定的标准如下：

对于单精度浮点(float)，最高位符号位，k = 8, n = 23。
对于双精度浮点(double), 最高位符号位，k = 11, n = 52。

具体编码和解码的时候我们分以下三种情况：

Normalized Values

这是最普遍的情况，这种情况发生的前提是指数部分不全为0或者1。因为二进制的指数部分e我们是按照无符号数表示，其需要表示指数值E为负的情况，所以这种情况下，我们约定E = e - Bias，其中Bias表示的值等于2^{k - 1} - 1，所以：

对于单精度，因为k = 8，Bias = 127，指数E的范围为-126 (1 - 127) ~ 127 (254 - 127)。
对于双精度，同理k = 11, Bias = 1023，指数E的范围为-1022 (1 - 1023) ~ 1023 (2046 - 1023)。

对于二进制的尾数部分f，其二进制表示为0.f_{n - 1}…f₁f₀，也就是说小数点是在最高位的左边，所以0 <= f < 1。但是对于M的值，我们默认前面有一个前导1，所以尾数部分真实表示的值为1.f_{n - 1}…f₁f₀，M = 1 + f，因而M的取值范围为1 <= M < 2。默认前导1的理由是在这种情况下，我们可以白嫖一位有效数字，不需要在f的部分去表示这个1。

Denormailized Values

这种情况的前提是指数部分全为0，这种情况下，我们约定指数部分的值为E = 1 - Bias。并且尾数部分没有前导1，所以M = f。Denormalized Values主要有两个作用:

表示0，指数和尾数部分全为0。需要注意+0和-0是不一样的，因为符号位有区别。
表示十分接近0的数。这个不难理解，因为指数部分已经十分小了 (单精度-126，双精度-1022)。

另外值得注意的一点事，约定E = 1 - Bias的原因是其和Normailzed Values的指数最小值一样，所以其保证了从Denomralized Values的最大值到Normalized Values最小值的平滑转换。

Special Values

这个情况发生在指数部分全为1的时候:

当尾数数部分全为0，根据符号位表示+∞或者-∞，无穷可以用来表示溢出。
当尾数部分不全为0的时候，表示NaN。

以上三种情况总结如下：

我们可以看出来这种表示方法的几个特点：

如果把浮点数映射到数轴上，我们可以看到其分布是随着其绝对值的变大而变稀疏的。这是因为相邻两个浮点数的间隔取决于指数E，E越小的话相邻两个浮点数的间隔越小；同理E越大的话，相邻两个浮点数的间隔越大：

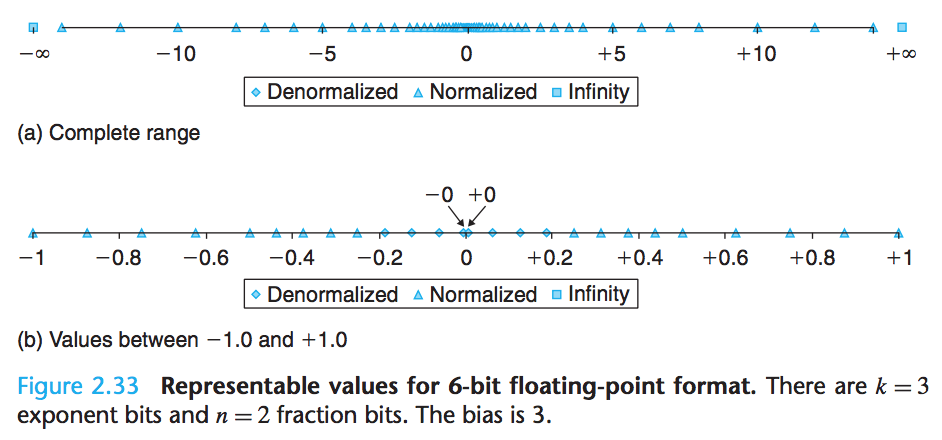
从Denormalized Values到Normalized Values的平滑转换是靠相同的E以及人为规定的有无默认前导1实现的：

另外如果二进制的表示更大的那个数，其真实的值也更大。

浮点数的表示范围

通过以上规则不难推断出浮点数的表示范围，我们以单精度举例（k = 8, n = 23）:

最大正数为s = 0, E = 127, M = (1.1111 1111 1111 1111 1111 111)₂的情况，约为3.402823e+38。
最小Normalized正数为s = 0, E = -126, M = (1.0000 0000 0000 0000 0000 000)₂，约为1.18 × 10^−38。
最小Denormalized正数为s = 0, E = -126, M = (0.0000 0000 0000 0000 0000 001)₂，约为1.4e-45。

负数同理。

浮点数的精度

浮点数转化成十进制之后的精度取决于尾数的最大值的位数，对于单精度而言，n = 23，所以M的最大值为 2²³ - 1 = 8388607，所以可以保证的精度为6位。

同理对于双精度，n = 52，M最大值为2⁵² - 1 = 4503599627370495，其可以保证的精度为15位。

浮点数的运算

浮点数的运算满足以下性质：

运算结果可能产生NaN或者Infinity。
运算满足交换律。
运算不满足结合律。
加法和乘法满足单调性。
除了NaN以及Infinity，任何数都有其相反数。

对于第三点，其根本原因是因为精度的舍入。例如(3.14 + 1e10) - 1e10的结果是0，然而3.14 + (1e10 - 1e10)的结果是3.14，因为3.14在和1e10相加的时候因为精度的问题被舍去了。因为这一点，我们在进行浮点数运算的时候需要极其注意。

对于单调性，我们定义如下：

对于加法，如果a >= b, 那么对于任何除了NaN的数x，a + x > = b + x。

对乘法，如果a > = b, 那么对于任何除了NaN的数x:

a * x >= b * x，当x >= 0 的时候。
a * x <= b * x，当x <= 0 的时候。

值得注意的一点是这种单调性对整数的加法和乘法是不满足的。

对于浮点数运算时的具体操作，我们用加法举例，假设存在两个浮点数x和y:

x = (-1)^s_x * M_x * 2^E_x
y = (-1)^s_y * M_y * 2^E_y

那么运算的结果为：

x + y = ((-1)^s_x * M_x * 2^{E_x - E_y} + (-1)^s_y M_y) 2^E_y

一般的运算步骤为：

对阶：把指数部分阶码对成一样，这样尾数部分经过移动后就可以直接相加。由于有效位数部分左移会丢失高位有效位，所以一般是采取右移，也就是小阶向大阶看齐。
尾数部分相加：无符号数相加。
规格化：若求和结果大于1，需要尾数右移一位，阶码加一。
舍入：右移出去的位，直接舍去。
检测溢出：检测阶码是否溢出。

另外我们回到之前的不满足结合律的例子 (3.14 + 1e10) - 1e10，其本质原因就是在对阶的过程中，要右移的位数过多，因为单精度总共才23位表示尾数，双精度52位，右移过多导致有效位数被舍入，所以导致了精度的缺失。